数学研究室
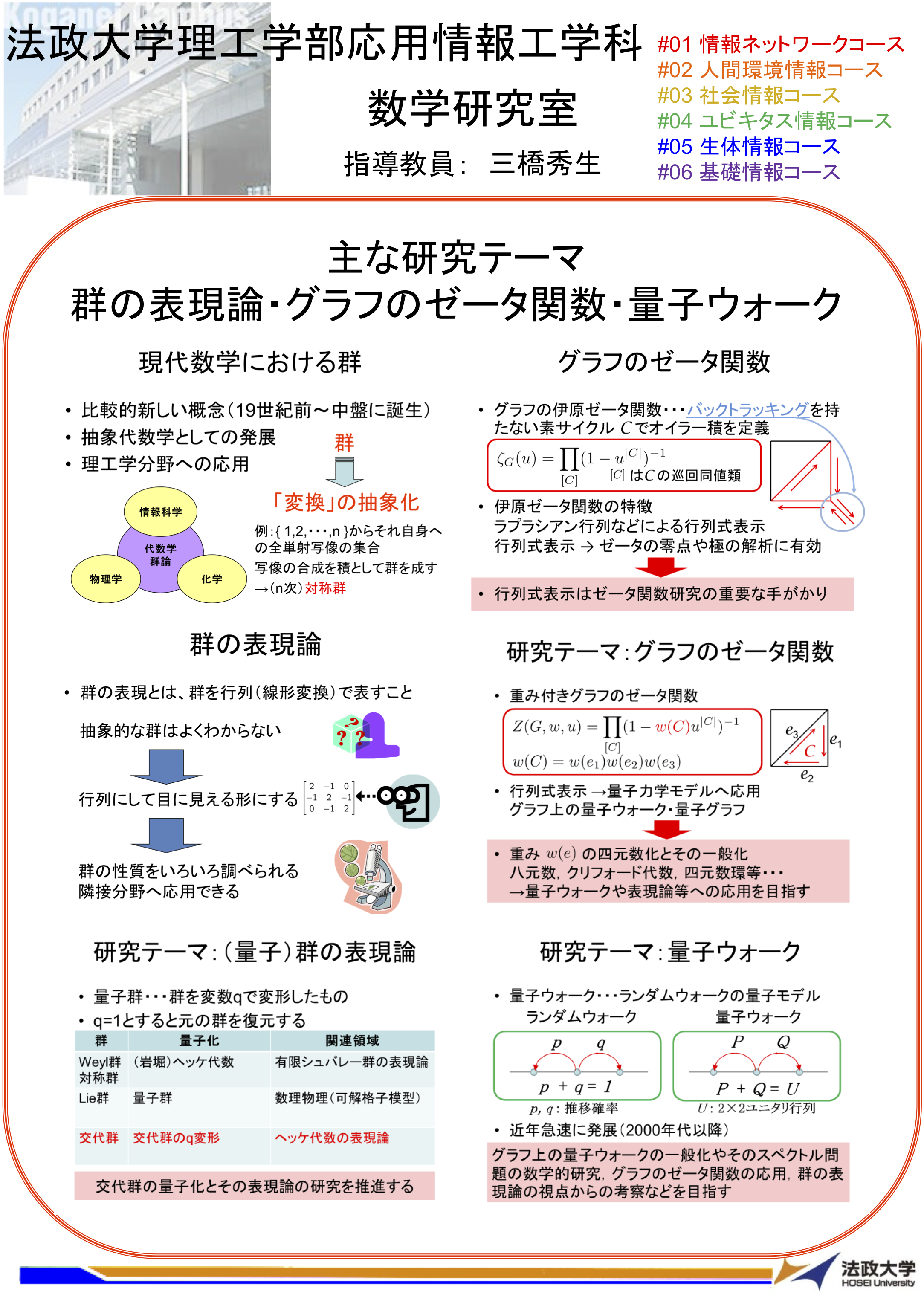
群の表現論,グラフのゼータ関数,量子ウォークが拓く数理の世界
ヘッケ代数や量子群の表現を代数的手法や組合せ論的手法で研究しています.また,グラフのゼータ関数の一般化,特に四元数重みをもつグラフのゼータ関数を研究しています.さらに,グラフ上の量子ウォークの四元数化やそのスペクトル問題を研究しています.そして、これらの数学分野を相互に応用しながら横断的な研究を進めています.
研究テーマ
担当科目
研究業績及び受賞歴
著書
学会活動・社会活動
学生の皆さんへのメッセージ
研究テーマ
対称群のヘッケ代数や交代群のヘッケ代数,及び量子群の表現論
四元数重み付きグラフのゼータ関数の構成と性質の究明および応用
グラフ上の量子ウォークの四元数化とそのスペクトル問題の解明
担当科目
【理工学部】
線形代数学演習I,線形代数学及び演習II,幾何学B,数学科教育法III,離散数学(情報),情報処理技法,情報工学ゼミナール、情報工学実験Ⅲ、PBL
研究業績及び受賞歴
著書
理科系の基礎 線形代数, 高遠節夫,石村隆一,野田健夫,前田多恵,三橋秀生,安冨真一,山方竜二,山下哲共著,培風館, (2015)
量子ウォークの新展開―数理構造の深化と応用,今野紀雄・井手勇介 共編著(第2章担当),培風館,(2019)
学会活動・社会活動
学生の皆さんへのメッセージ
みなさんには,法政大学での研鑽を通じて,科学技術と数学に深い造詣と探究心を持ち,実践と理論を兼ね備えた人材になってもらいたいと思っています.そして,幅広い教養と深い専門性を持った,立派な社会人になってほしいです.